InvestGrow EasyMining is similar to solo mining with an ASIC, but with a key difference: instead of using your own hardware, you're purchasing hashing power for a specific period of time. During that time frame, you have the opportunity to find a block and earn the full block reward, just like in solo mining.
However, unlike traditional solo mining, NiceHash offers flexible packages with different levels of hashing power. You can choose a smaller, more affordable package with lower probability of finding a block, or invest in a larger package with higher hashrate, significantly increasing your probability of success but at a higher cost. This flexibility allows users to tailor their risk and reward based on their budget. An added benefit is that you can potentially confirm multiple blocks within a single purchased package, maximizing your returns during the package lifetime.
Probability of finding a block
The probability of finding a valid block over a given period can be approximated by comparing the miner's effective hashrate with the network's total hashrate and factoring in the block time.
The formula is:
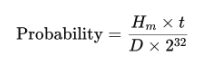
This method provides a rough estimate, but in reality, mining involves more variables, and actual probabilities can be influenced by other factors like changes in network difficulty, timing, etc,...
Network Difficulty [D]: is a measure of how hard it is to find a new block (i.e., solve the Proof of Work problem) on the blockchain. It's adjusted based on how quickly miners are solving blocks, ensuring a consistent block time (e.g., around 10 minutes for Bitcoin).
Hashrate [Hm]: is the total computational power (measured in hashes per second) that is being used to mine cryptocurrency on the network. It measures how many hashes (attempts) miners are making per second to solve a block.
To calculate hashrate from network difficulty, you multiply the difficulty by 2³² and divide by the block time in seconds. For Bitcoin, the block time is typically 600 seconds, but it varies for other cryptocurrencies.
Here's a mathematical approach to get a probability of finding a block:

- Let Hm be the miner’s hashrate (hashes per second).
- Let D be the network difficulty.
- Let t be the time spent mining (in seconds).
1. The total number of hashes the miner will compute over time t is:
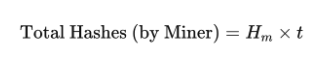
2. The average number of hashes needed to find a valid block, given the network difficulty, is:
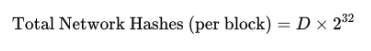
3. And finally the probability that a miner will find a valid block in the given time t is the ratio of the hashes your miner can compute versus the total number of hashes required to find a block on the network:
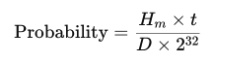
Example Calculation:
Let’s assume the following:
- Miner’s hashrate Hm = 3,000 TH/s = 3 PH/s
- Network difficulty D = 90 trillion (90,000,000,000,000) = 90 × 1012
- Mining time t = 1 hour = 3,600 seconds.
This is a rough estimate for buying a Gold S package (0.0001 BTC) for a duration of 1 hour at a hashrate price: 0.7 BTC/EH/s. The resulting package hashrate is:
Hm = 0.0001 / (0.7 / 24) = 0.003 EH/s = 3 PH/s
Miner’s Total Hashes in 1 hour:
3 PH/s × 3,600 s = 10.8 EH = 10.8 × 1018 H
Total Network Hashes required to find a block (on average every 10 minutes):
(90 × 1012) × 232 ≈ 3.865 × 1023
Probability of finding a block::
Probability ≈ 10.8 × 1018 / 3.865 × 1023 ≈ 0.000028
This means the probability of winning a Bitcoin block with 3 PH/s over the course of 1 hour is roughly 0.0028% or 1 : 35.787
Advanced mathematical approach to calculating probabilities of finding at least one block
The Poisson distribution is especially useful for calculating the probability of rare events occurring over a fixed period, such as confirming a Bitcoin block. Mining is an ideal example of a Poisson process since the discovery of each block is independent of the others, and blocks are found at a constant average rate, determined by hashrate or difficulty.
The Poisson distribution models the likelihood of a specific number of events occurring within a fixed interval, assuming the events happen at a constant average rate. The formula for the probability of observing k events in a given time period is:
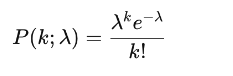
Where:
- P(k;λ) is the probability of observing k events (blocks in our case) over a time interval.
- λ is the expected number of events (the average rate of events over the interval).
- e is Euler’s number (~2.71828).
- k is the number of events you are interested in (e.g., k=1 for finding exactly one block).
For mining, λ is the expected number of blocks found in the time period based on your hashrate. The expected number of blocks (λ) that a miner with hashrate Hm can find in a given period t is:
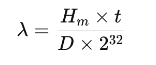
Where:
- Hm the miner's hashrate (in hashes per second).
- t is the mining time (in seconds).
- D is the network difficulty.
- 2³² is an offset factor for difficulty
Using the Poisson formula, the probability of finding exactly one block (k=1) is:
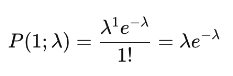
The probability of finding at least one block can be calculated as the complement of finding zero blocks:
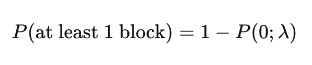
Where P(0; λ) is the probability of finding zero blocks, calculated as:
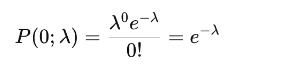
Thus, the final formula for the probability of finding at least one block becomes:

Note: This formula is used to calculate the probabilities of all EasyMining packages.
Example Calculation:
Let’s assume the following:
- Miner’s hashrate Hm = 3,000 TH/s = 3 PH/s
- Network difficulty D = 90 trillion (90,000,000,000,000) = 90 × 1012
- Mining time t = 1 hour = 3,600 seconds.
λ = 10.8 × 1018 / 3.865 × 1023 ≈ 0.000028
P(at least 1 block) = 1 - e-0.000028 ≈ 0.000028
For small λ, e-λ ≈ 1 - λ. Therefore, the probability of finding at least one block becomes:
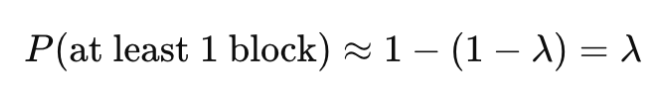
The probability of finding at least one block is approximately λ, which depends on the miner's hashrate, the network difficulty, and the time spent mining.






